K均值聚类 | k-means clustering
什么是聚类算法
众所周知,机器学习算法可分为监督学习(Supervised learning)和无监督学习(Unsupervised learning)。
监督学习常用于分类和预测。是让计算机去学习已经创建好的分类模型,使分类(预测)结果更好的接近所给目标值,从而对未来数据进行更好的分类和预测。因此,数据集中的所有变量被分为特征和目标,对应模型的输入和输出;数据集被分为训练集和测试集,分别用于训练模型和模型测试与评估。常见的监督学习算法有Regression(回归)、KNN和SVM(分类)。
无监督学习常用于聚类。输入数据没有标记,也没有确定的结果,而是通过样本间的相似性对数据集进行聚类,使类内差距最小化,类间差距最大化。无监督学习的目标不是告诉计算机怎么做,而是让它自己去学习怎样做事情,去分析数据集本身。常用的无监督学习算法有K-means、 PCA(Principle Component Analysis)。
扩展阅读:
《一文看懂机器学习!(3种学习方法+7个实操步骤+15种常见算法)》
聚类算法又叫做“无监督分类”,其目的是将数据划分成有意义或有用的组(或簇)。这种划分可以基于业务需求或建模需求来完成,也可以单纯地帮助我们探索数据的自然结构和分布。比如在商业中,如果手头有大量的当前和潜在客户的信息,可以使用聚类将客户划分为若干组,以便进一步分析和开展营销活动。再比如,聚类可以用于降维和矢量量化,可以将高维特征压缩到一列当中,常常用于图像、声音和视频等非结构化数据,可以大幅度压缩数据量。
聚类算法与分类算法的比较:

K-Means详细介绍
1. K-Means的工作原理
作为聚类算法的典型代表,K-Means可以说是最简单的聚类算法,那它的聚类工作原理是什么呢?

在K-Means算法中,簇的个数K是一个超参数,需要人为输入来确定。K-Means的核心任务就是根据设定好的K,找出K个最优的质心,并将离这些质心最近的数据分别分配到这些质心代表的簇中去。具体过程可以总结如下:
首先随机选取样本中的K个点作为聚类中心;
分别算出样本中其他样本距离这K个聚类中心的距离,并把这些样本分别作为自己最近的那个聚类中心的类别;
对上述分类完的样本再进行每个类别求平均值,求解出新的聚类质心;
与前一次计算得到的K个聚类质心比较,如果聚类质心发生变化,转过程b,否则转过程e;
当质心不发生变化时(当我们找到一个质心,在每次迭代中被分配到这个质心上的样本都是一致的,即每次新生成的簇都是一致的,所有的样本点都不会再从一个簇转移到另一个簇,质心就不会变化了),停止并输出聚类结果。K-Means算法计算过程如下图所示:
 K-Means算法计算过程
K-Means算法计算过程
例题:
对于以下数据点,请采用k-means方法进行聚类(手工计算)。假设聚类簇数k=3,初始聚类簇中心分别为数据点2、数据点3、数据点5。
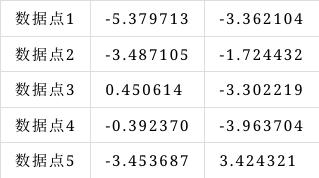
解:
正在进行第1次迭代初始质心为B、C、E
AB = 2.502785
AC = 5.830635
AE = 7.054443
DB = 3.819911
DC = 1.071534
DE = 7.997158
因此,第一簇:{A,B};第二簇:{C,D};第三簇:{E}
即[
array([-5.379713, -3.362104]),
array([-3.487105, -1.724432])][array([ 0.450614, -3.302219]),
array([-0.39237, -3.963704])][array([-3.45368, 3.424321])
]
所以:
第一簇的质心为F:[-4.433409 -2.543268]
第二簇的质心为G:[ 0.029122 -3.6329615]
第三簇的质心为H:[-3.45368 3.424321]
###########################################################
正在进行第2次迭代
AF = 1.251393
AG = 5.415613
AH = 7.054443
BF = 1.251393
BG = 4.000792
BH = 5.148861
CF = 4.942640
CG = 0.535767
CH = 7.777522
DF = 4.283414
DG = 0.535767
DH = 7.997158
EF = 6.047478
EG = 7.869889
EH = 0.000000
因此,第一簇:{A,B};第二簇:{C,D};第三簇:{E}
即[
array([-5.379713, -3.362104]),
array([-3.487105, -1.724432])][array([ 0.450614, -3.302219]),
array([-0.39237, -3.963704])][array([-3.45368, 3.424321])
]
所以:
第一簇的质心为:[-4.433409 -2.543268]
第二簇的质心为:[ 0.029122 -3.6329615]
第三簇的质心为:[-3.45368 3.424321]
###########################################################
由于三个簇的成员保持不变,聚类结束
综上所述:第一簇:{A,B};第二簇:{C,D};第三簇:{E}
2. 簇内误差平方和的定义
聚类算法聚出的类有什么含义呢?这些类有什么样的性质?
我们认为,被分在同一个簇中的数据是有相似性的,而不同簇中的数据是不同的,当聚类完毕之后,接下来需要分别研究每个簇中的样本都有什么样的性质,从而根据业务需求制定不同的商业或者科技策略。聚类算法追求“簇内差异小,簇外差异大”。而这个 “差异”便是通过样本点到其簇质心的距离来衡量。
对于一个簇来说,所有样本点到质心的距离之和越小,便认为这个簇中的样本越相似,簇内差异越小。而距离的衡量方法有多种,令x表示簇中的一个样本点,μ表示该簇中的质心,n表示每个样本点中的特征数目,i表示组成点x的每个特征,则该样本点到质心的距离可以由以下距离来度量:

如采用欧几里得距离,则一个簇中所有样本点到质心的距离的平方和为:

其中,m为一个簇中样本的个数,j是每个样本的编号。这个公式被称为簇内平方和(Cluster Sum of Square),又叫做Inertia。而将一个数据集中的所有簇的簇内平方和相加,就得到了整体平方和(Total Cluster Sum of Square),又叫做Total Inertia。Total Inertia越小,代表着每个簇内样本越相似,聚类的效果就越好。因此K-Means追求的是:求解能够让Inertia最小化的质心。实际上,在质心不断变化不断迭代的过程中,总体平方和是越来越小的。我们可以通过数学来证明,当整体平方和达到最小值的时候,质心就不再发生变化了。如此,K-Means的求解过程,就变成了一个最优化问题。
在K-Means中,在一个固定的簇数K条件下,最小化总体平方和来求解最佳质心,并基于质心的存在去进行聚类。两个过程十分相似,并且整体距离平方和的最小值其实可以使用梯度下降来求解。
大家可以发现, Inertia是基于欧几里得距离的计算公式得来的。实际上,也可以使用其他距离,每个距离都有自己对应的Inertia。在过去的经验中,已经总结出不同距离所对应的质心选择方法和Inertia,在K-Means中,只要使用了正确的质心和距离组合,无论使用什么距离,都可以达到不错的聚类效果。

3. K-Means算法的时间复杂度
众所周知,算法的复杂度分为时间复杂度和空间复杂度,时间复杂度是指执行算法所需要的计算工作量,常用大O符号表述;而空间复杂度是指执行这个算法所需要的内存空间。如果一个算法的效果很好,但需要的时间复杂度和空间复杂度都很大,那将会在算法的效果和所需的计算成本之间进行权衡。
K-Means算法是一个计算成本很大的算法。K-Means算法的平均复杂度是O(k*n*T),其中k是超参数,即所需要输入的簇数,n是整个数据集中的样本量,T是所需要的迭代次数。在最坏的情况下,KMeans的复杂度可以写作O(n(k+2)/p),其中n是整个数据集中的样本量,p是特征总数。
4. 聚类算法的模型评估指标
不同于分类模型和回归,聚类算法的模型评估不是一件简单的事。在分类中,有直接结果(标签)的输出,并且分类的结果有正误之分,所以需要通过使用预测的准确度、混淆矩阵、ROC曲线等指标来进行评估,但无论如何评估,都是在评估“模型找到正确答案”的能力。而在回归中,由于要拟合数据,可以通过SSE均方误差、损失函数来衡量模型的拟合程度。但这些衡量指标都不能够用于聚类。
聚类模型的结果不是某种标签输出,并且聚类的结果是不确定的,其优劣由业务需求或者算法需求来决定,并且没有永远的正确答案。那如何衡量聚类的效果呢?
K-Means的目标是确保“簇内差异小,簇外差异大”,所以可以通过衡量簇内差异来衡量聚类的效果。前面讲过,Inertia是用距离来衡量簇内差异的指标,因此,是否可以使用Inertia来作为聚类的衡量指标呢?
「肘部法(手肘法)认为图3的拐点就是k的最佳值」
手肘法核心思想:随着聚类数k的增大,样本划分会更加精细,每个簇的聚合程度会逐渐提高,那么Inertia自然会逐渐变小。当k小于真实聚类数时,由于k的增大会大幅增加每个簇的聚合程度,故Inertia的下降幅度会很大,而当k到达真实聚类数时,再增加k所得到的聚合程度回报会迅速变小,所以Inertia的下降幅度会骤减,然后随着k值的继续增大而趋于平缓,也就是说Inertia和k的关系图是一个手肘的形状,而这个肘部对应的k值就是数据的真实聚类数。例如下图,肘部对于的k值为3(曲率最高),故对于这个数据集的聚类而言,最佳聚类数应该选3。

那就引出一个问题:Inertia越小模型越好吗?答案是可以的,但是Inertia这个指标又有其缺点和极限:
它的计算太容易受到特征数目的影响。
它不是有界的,Inertia是越小越好,但并不知道何时达到模型的极限,能否继续提高。
它会受到超参数K的影响,随着K越大,Inertia必定会越来越小,但并不代表模型效果越来越好。
Inertia 对数据的分布有假设,它假设数据满足凸分布,并且它假设数据是各向同性的,所以使用Inertia作为评估指标,会让聚类算法在一些细长簇、环形簇或者不规则形状的流形时表现不佳。
那又可以使用什么指标来衡量模型效果呢?
(1)轮廓系数
在99%的情况下,是对没有真实标签的数据进行探索,也就是对不知道真正答案的数据进行聚类。这样的聚类,是完全依赖于评价簇内的稠密程度(簇内差异小)和簇间的离散程度(簇外差异大)来评估聚类的效果。其中轮廓系数是最常用的聚类算法的评价指标。它是对每个样本来定义的,它能够同时衡量:
样本与其自身所在的簇中的其他样本的相似度a,等于样本与同一簇中所有其他点之间的平均距离。
样本与其他簇中的样本的相似度b,等于样本与下一个最近的簇中的所有点之间的平均距离。
根据聚类“簇内差异小,簇外差异大”的原则,我们希望b永远大于a,并且大得越多越好。单个样本的轮廓系数计算为:

公式进行展开为:

很容易理解轮廓系数范围是(-1,1),其中值越接近1表示样本与自己所在的簇中的样本很相似,并且与其他簇中的样本不相似,当样本点与簇外的样本更相似的时候,轮廓系数就为负。当轮廓系数为0时,则代表两个簇中的样本相似度一致,两个簇本应该是一个簇。
如果一个簇中的大多数样本具有比较高的轮廓系数,簇会有较高的总轮廓系数,则整个数据集的平均轮廓系数越高,表明聚类是合适的;如果许多样本点具有低轮廓系数甚至负值,则聚类是不合适的,聚类的超参数K可能设定得太大或者太小。
轮廓系数有很多优点,它在有限空间中取值,使得我们对模型的聚类效果有一个“参考”。并且,轮廓系数对数据的分布没有限定,因此在很多数据集上都表现良好,它在每个簇的分割比较清晰时表现最好。但轮廓系数也有缺陷,它在凸型的类上表现会虚高,比如基于密度进行的聚类,或通过DBSCAN获得的聚类结果,如果使用轮廓系数来衡量,则会表现出比真实聚类效果更高的分数。
(2)卡林斯基-哈拉巴斯指数
除了最常用的轮廓系数,还有卡林斯基-哈拉巴斯指数(Calinski-Harabaz Index,简称CHI,也被称为方差比标准)、戴维斯-布尔丁指数(Davies-Bouldin)以及权变矩阵(Contingency Matrix)可以使用。在这里不多介绍,感兴趣的读者可以自己学习。
5. 初始质心的问题
在K-Means中有一个重要的环节,就是放置初始质心。如果有足够的时间,K-means一定会收敛,但Inertia可能收敛到局部最小值。是否能够收敛到真正的最小值很大程度上取决于质心的初始化。
初始质心放置的位置不同,聚类的结果很可能也会不一样,一个好的质心选择可以让K-Means避免更多的计算,让算法收敛稳定且更快。在之前讲解初始质心的放置时,是采用“随机”的方法在样本点中抽取k个样本作为初始质心,这种方法显然不符合“稳定且更快”的需求。
为此,在sklearn中使用random_state参数来实现控制,确保每次生成的初始质心都在相同位置,甚至可以画学习曲线来确定最优的random_state参数。
一个random_state对应一个质心随机初始化的随机数种子。如果不指定随机数种子,则sklearn中的K-Means并不会只选择一个随机模式扔出结果,而会在每个随机数种子下运行多次,并使用结果最好的一个随机数种子来作为初始质心。
在sklearn中也可以使用参数n_init来选择(每个随机数种子下运行的次数),可以增加这个参数n_init的值来增加每个随机数种子下运行的次数。
另外,为了优化选择初始质心的方法,“k-means ++”能够使得初始质心彼此远离,以此来引导出比随机初始化更可靠的结果。在sklearn中,使用参数init =‘k-means ++'来选择使用k-means++作为质心初始化的方案。
6. 聚类算法的迭代问题
大家都知道,当质心不再移动,Kmeans算法就会停下来。在完全收敛之前,sklearn中也可以使用max_iter(最大迭代次数)或者tol两个参数来让迭代提前停下来。有时候,当n_clusters选择不符合数据的自然分布,或者为了业务需求,必须要填入n_clusters数据提前让迭代停下来时,反而能够提升模型的表现。
max_iter:整数,默认300,单次运行的k-means算法的最大迭代次数;
tol:浮点数,默认1e-4,两次迭代间Inertia下降的量,如果两次迭代之间Inertia下降的值小于tol所设定的值,迭代就会停下。
K-Means算法的优缺点
K-Means算法优点:
算法简单,容易实现 ;
算法速度很快;
对处理大数据集,该算法是相对可伸缩的和高效率的,因为它的复杂度大约是O(nkt),其中n是所有对象的数目,k是簇的数目,t是迭代的次数。通常k<<n。这个算法通常局部收敛。
算法尝试找出使平方误差函数值最小的k个划分。当簇是密集的、球状或团状的,且簇与簇之间区别明显时,聚类效果较好。
K-Means算法缺点:
对数据类型要求较高,适合数值型数据;
可能收敛到局部最小值,在大规模数据上收敛较慢
分组的数目k是一个输入参数,不合适的k可能返回较差的结果。
对初值的簇心值敏感,对于不同的初始值,可能会导致不同的聚类结果;
不适合于发现非凸面形状的簇,或者大小差别很大的簇。
对于”噪声”和孤立点数据敏感,少量的该类数据能够对平均值产生极大影响。
结论
K均值(K-Means)聚类算法原理简单,可解释强,实现方便,可广泛应用在数据挖掘、聚类分析、数据聚类、模式识别、金融风控、数据科学、智能营销和数据运营等多个领域,有着广泛的应用前景。
百科介绍
百度百科(详情)
K均值聚类算法是先随机选取K个对象作为初始的聚类中心。然后计算每个对象与各个种子聚类中心之间的距离,把每个对象分配给距离它最近的聚类中心。聚类中心以及分配给它们的对象就代表一个聚类。一旦全部对象都被分配了,每个聚类的聚类中心会根据聚类中现有的对象被重新计算。这个过程将不断重复直到满足某个终止条件。终止条件可以是没有(或最小数目)对象被重新分配给不同的聚类,没有(或最小数目)聚类中心再发生变化,误差平方和局部最小。
维基百科(详情)
ķ -means聚类是的方法的矢量量化,最初来自信号处理,即流行聚类分析在数据挖掘。ķ -means聚类的目的是划分 Ñ观测到 ķ其中每个观测属于簇群集与最近的平均值,作为原型群集的。这导致数据空间划分为 Voronoi单元。
问题在计算上很困难(NP难); 然而,有效的启发式算法快速收敛到局部最优。这些通常是类似于最大期望算法为混合物的高斯分布经由通过两个采用的迭代细化方法k-均值和高斯混合模型。他们都使用集群中心来建模数据; 然而,k -means聚类倾向于找到具有可比空间范围的聚类,而期望最大化机制允许聚类具有不同的形状。
该算法与k最近邻分类器有松散的关系,这是一种流行的分类机器学习技术,由于名称的原因,它经常与k -means 混淆。应用1最近邻分类器,通过k -means 获得的聚类中心将新数据分类到现有聚类中。这被称为最近的质心分类器或Rocchio算法。